Transformer from Scratch

Explaining and Implementing Transformer from Scratch.
Transformer
Author

Madhav Kanda

Published

December 7, 2025

Transformer from Scratch

This single notebook walks through the core building blocks of a GPT-style Transformer as implemented from scratch.

Outline:

  • Positional encodings
  • Causal mask utility
  • Self-attention from first principles
  • Single-head self-attention
  • Multi-head self-attention
  • Feed-Forward network (GELU)
  • Transformer block (LayerNorm → MHA → residual → LayerNorm → FFN → residual)
  • Shape walkthrough and a quick visualization

Notation legend used throughout:

  • B: batch size
  • T: sequence length
  • d_model (a.k.a. C): embedding size
  • H (a.k.a. n_head): number of attention heads
  • d_head (a.k.a. D): per-head size, d_model / H

Setup and imports

We will use NumPy for a didactic, tiny attention example and PyTorch for the full modules.

Less-familiar PyTorch utilities referenced below:

  • nn.Linear(in, out): affine projection along the last dimension
  • nn.LayerNorm(d_model): normalizes features in the last dimension
  • F.softmax(x, dim=-1): softmax over the last dimension
  • Tensor.view(...): reshape without copy (requires contiguous() memory)
  • Tensor.transpose(dim0, dim1): swap two dimensions
  • Tensor.contiguous(): ensure contiguous memory layout so view can work
  • Tensor.masked_fill(mask, value): set entries where mask==True to value
  • register_buffer(name, tensor): attach non-parameter tensors (e.g., constants) to modules so they move with the device and save in checkpoints
import math
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F

torch.manual_seed(0)
<torch._C.Generator at 0x7fe60b34aff0>

Positional encodings

Goal: inject token position information into embeddings so the model knows order.

Shapes:

  • Input x: (B, T, d_model)
  • Positional table pe: (max_len, d_model)
  • Sliced positions pe[:T]: (T, d_model) → unsqueeze(0) → (1, T, d_model), broadcast to (B, T, d_model)

Flow (sinusoidal implementation):

  1. Build a fixed pe of size (max_len, d_model) using sin/cos at geometrically spaced frequencies:
    • for even dims: sin(position · 10000^{-2i/d_model})
    • for odd dims: cos(position · 10000^{-2i/d_model})
  2. In forward, slice pe[:T], add a batch axis, and return x + pe[:T].
class SinusoidalPositionalEncoding(nn.Module):
    def __init__(self, max_len: int, d_model: int):
        super().__init__()
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model)
        )
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        self.register_buffer("pe", pe)

    def forward(self, x: torch.Tensor):
        B, T, _ = x.shape
        return x + self.pe[:T].unsqueeze(0)
# Quick sanity check
B, T, d_model = 2, 4, 8
x = torch.randn(B, T, d_model)
sep = SinusoidalPositionalEncoding(max_len=128, d_model=d_model)
print("SEP:", sep(x).shape)
SEP: torch.Size([2, 4, 8])

Causal mask

We prevent a token at time t from attending to future tokens > t.

Shapes and broadcasting:

  • Returned mask: (1, 1, T, T) with True above the main diagonal
  • Attention scores: (B, H, T, T)
  • PyTorch will broadcast (1,1,T,T) across (B,H,T,T) when we call masked_fill

Flow:

  1. Build an upper-triangular boolean matrix with torch.triu(..., diagonal=1)
  2. Reshape to (1,1,T,T) so it broadcasts cleanly over batch and heads
def causal_mask(T: int, device=None):
    m = torch.triu(torch.ones((T, T), dtype=torch.bool, device=device), diagonal=1)
    return m.view(1, 1, T, T)


print("Mask shape:", causal_mask(4).shape)
Mask shape: torch.Size([1, 1, 4, 4])

Self-attention from first principles

Shapes (single head):

  • X: (1, T=3, d_model=4)
  • Wq/Wk/Wv: (d_model=4, d_k=2)
  • Q, K, V: (1, 3, 2)
  • scores Q @ K^T: (1, 3, 3)
  • weights: (1, 3, 3) after softmax over the last dim
  • output: (1, 3, 2) = weights @ V

Flow:

  1. Linear projections: Q=XWq, K=XWk, V=XWv
  2. Scale: divide by sqrt(d_k) for stable gradients
  3. Mask: set strictly upper triangle to -1e9 (≈-inf) so softmax→0 for future
  4. Softmax: normalized along the last dimension (per query position)
  5. Weighted sum: weights @ V

Notes:

  • We subtract the rowwise max before exp to avoid overflow (softmax trick).
  • NumPy broadcasting mirrors PyTorch here; the PyTorch version adds dropout and more heads.
# Tiny NumPy self-attention demo
X = np.array(
    [[[0.1, 0.2, 0.3, 0.4], [0.5, 0.4, 0.3, 0.2], [0.0, 0.1, 0.0, 0.1]]],
    dtype=np.float32,
)

Wq = np.array([[0.2, -0.1], [0.0, 0.1], [0.1, 0.2], [-0.1, 0.0]], dtype=np.float32)
Wk = np.array([[0.1, 0.1], [0.0, -0.1], [0.2, 0.0], [0.0, 0.2]], dtype=np.float32)
Wv = np.array([[0.1, 0.0], [-0.1, 0.1], [0.2, -0.1], [0.0, 0.2]], dtype=np.float32)

Q = X @ Wq
K = X @ Wk
V = X @ Wv
print("Q shape:", Q.shape, "\nQ=\n", Q[0])
print("K shape:", K.shape, "\nK=\n", K[0])
print("V shape:", V.shape, "\nV=\n", V[0])

scale = 1.0 / np.sqrt(Q.shape[-1])
attn_scores = (Q @ K.transpose(0, 2, 1)) * scale
mask = np.triu(np.ones((1, 3, 3), dtype=bool), k=1)
attn_scores = np.where(mask, -1e9, attn_scores)

weights = np.exp(attn_scores - attn_scores.max(axis=-1, keepdims=True))
weights = weights / weights.sum(axis=-1, keepdims=True)
print("Weights shape:", weights.shape, "\nAttention Weights (causal)=\n", weights[0])

out = weights @ V
print("Output shape:", out.shape, "\nOutput=\n", out[0])
Q shape: (1, 3, 2) 
Q=
 [[ 0.01        0.07      ]
 [ 0.11000001  0.05      ]
 [-0.01        0.01      ]]
K shape: (1, 3, 2) 
K=
 [[0.07       0.07      ]
 [0.11000001 0.05      ]
 [0.         0.01      ]]
V shape: (1, 3, 2) 
V=
 [[ 0.05  0.07]
 [ 0.07  0.05]
 [-0.01  0.03]]
Weights shape: (1, 3, 3) 
Attention Weights (causal)=
 [[1.         0.         0.        ]
 [0.49939896 0.50060104 0.        ]
 [0.33337261 0.3332312  0.33339619]]
Output shape: (1, 3, 2) 
Output=
 [[0.05       0.07      ]
 [0.06001202 0.05998798]
 [0.03666085 0.04999953]]

Single-head self-attention (PyTorch)

Shapes:

  • Input x: (B, T, d_model)
  • q, k, v: (B, T, d_k)
  • scores q @ k^T: (B, T, T)
  • weights: (B, T, T) (softmax over last dim)
  • output: (B, T, d_k)

Flow of the code below:

  1. Linear projections: three nn.Linear(d_model → d_k) for Q/K/V
  2. Scores: q @ k.transpose(-2, -1) then scale by 1/sqrt(d_k)
  3. Causal mask: masked_fill(mask.squeeze(1), -inf) so future gets prob 0
  4. Softmax over last dim → attention weights
  5. Dropout on weights (regularization)
  6. Weighted sum with v → head output

PyTorch utilities used:

  • transpose(-2, -1): swap the last two dims to get (B, T, d_k)^T → (B, d_k, T) for matmul
  • F.softmax(..., dim=-1): normalize across keys for each query
  • Dropout: randomly zeroes some probabilities at train-time
class SingleHeadSelfAttention(nn.Module):
    def __init__(
        self, d_model: int, d_k: int, dropout: float = 0.0, trace_shapes: bool = False
    ):
        super().__init__()
        self.q = nn.Linear(d_model, d_k, bias=False)
        self.k = nn.Linear(d_model, d_k, bias=False)
        self.v = nn.Linear(d_model, d_k, bias=False)
        self.dropout = nn.Dropout(dropout)
        self.trace_shapes = trace_shapes

    def forward(self, x: torch.Tensor):  # x: (B, T, d_model)
        B, T, _ = x.shape
        q = self.q(x)
        k = self.k(x)
        v = self.v(x)
        if self.trace_shapes:
            print(f"q {q.shape}  k {k.shape}  v {v.shape}")
        scale = 1.0 / math.sqrt(q.size(-1))
        attn = torch.matmul(q, k.transpose(-2, -1)) * scale  # (B,T,T)
        mask = causal_mask(T, device=x.device)
        attn = attn.masked_fill(mask.squeeze(1), float("-inf"))
        w = F.softmax(attn, dim=-1)
        w = self.dropout(w)
        out = torch.matmul(w, v)  # (B,T,d_k)
        if self.trace_shapes:
            print(f"weights {w.shape}  out {out.shape}")
        return out, w


# Quick demo
B, T, d_model, d_k = 2, 5, 12, 4
x = torch.randn(B, T, d_model)
head = SingleHeadSelfAttention(d_model, d_k, trace_shapes=True)
out, w = head(x)
print("Single head out:", out.shape, "weights:", w.shape)
q torch.Size([2, 5, 4])  k torch.Size([2, 5, 4])  v torch.Size([2, 5, 4])
weights torch.Size([2, 5, 5])  out torch.Size([2, 5, 4])
Single head out: torch.Size([2, 5, 4]) weights: torch.Size([2, 5, 5])

Multi-head self-attention (PyTorch)

Shapes (C ≡ d_model, H ≡ n_head, D ≡ d_head=C/H):

  • Input x: (B, T, C)
  • qkv = Linear(x): (B, T, 3C)
  • view → (B, T, 3, H, D) then unbind → q,k,v: (B, T, H, D)
  • transpose(1,2): q,k,v → (B, H, T, D)
  • scores q @ k^T: (B, H, T, T) → softmax weights (B, H, T, T)
  • context weights @ v: (B, H, T, D)
  • merge heads: transpose(1,2).contiguous().view(B, T, C)
  • final projection: (B, T, C)

Flow of the code below:

  1. Single linear layer produces concatenated Q|K|V for all heads
  2. Reshape and split into per-head tensors; swap to (B,H,T,D) for batched matmul
  3. Compute scaled dot-product attention with causal masking
  4. Combine per-head contexts back to (B,T,C) and apply a final linear projection

PyTorch details:

  • view requires contiguous memory; hence contiguous() before view
  • The (1,1,T,T) mask broadcasts to (B,H,T,T) in masked_fill
  • We assert d_model % n_head == 0 so all heads have equal size
class MultiHeadSelfAttention(nn.Module):
    def __init__(
        self,
        d_model: int,
        n_head: int,
        dropout: float = 0.0,
        trace_shapes: bool = False,
    ):
        super().__init__()
        assert d_model % n_head == 0, "d_model must be divisible by n_head"
        self.n_head = n_head
        self.d_head = d_model // n_head
        self.qkv = nn.Linear(d_model, 3 * d_model, bias=False)
        self.proj = nn.Linear(d_model, d_model, bias=False)
        self.dropout = nn.Dropout(dropout)
        self.trace_shapes = trace_shapes

    def forward(self, x: torch.Tensor):  # (B,T,d_model)
        B, T, C = x.shape
        qkv = self.qkv(x)  # (B,T,3*C)
        qkv = qkv.view(B, T, 3, self.n_head, self.d_head)  # (B,T,3,H,D)
        if self.trace_shapes:
            print("qkv view:", qkv.shape)
        q, k, v = qkv.unbind(dim=2)  # each (B,T,H,D)
        q = q.transpose(1, 2)  # (B,H,T,D)
        k = k.transpose(1, 2)
        v = v.transpose(1, 2)
        if self.trace_shapes:
            print("q:", q.shape, "k:", k.shape, "v:", v.shape)
        scale = 1.0 / math.sqrt(self.d_head)
        attn = torch.matmul(q, k.transpose(-2, -1)) * scale  # (B,H,T,T)
        mask = causal_mask(T, device=x.device)
        attn = attn.masked_fill(mask, float("-inf"))
        w = F.softmax(attn, dim=-1)
        w = self.dropout(w)
        ctx = torch.matmul(w, v)  # (B,H,T,D)
        if self.trace_shapes:
            print("weights:", w.shape, "ctx:", ctx.shape)
        out = ctx.transpose(1, 2).contiguous().view(B, T, C)  # (B,T,C)
        out = self.proj(out)
        if self.trace_shapes:
            print("out:", out.shape)
        return out, w


# Quick demo
B, T, d_model, n_head = 2, 5, 12, 3
x = torch.randn(B, T, d_model)
mha = MultiHeadSelfAttention(d_model, n_head, trace_shapes=True)
out, w = mha(x)
print("MHA out:", out.shape, "weights:", w.shape)
qkv view: torch.Size([2, 5, 3, 3, 4])
q: torch.Size([2, 3, 5, 4]) k: torch.Size([2, 3, 5, 4]) v: torch.Size([2, 3, 5, 4])
weights: torch.Size([2, 3, 5, 5]) ctx: torch.Size([2, 3, 5, 4])
out: torch.Size([2, 5, 12])
MHA out: torch.Size([2, 5, 12]) weights: torch.Size([2, 3, 5, 5])

Feed-Forward network

Position-wise MLP applied independently at each sequence position.

Shapes:

  • Input: (B, T, d_model)
  • Hidden: (B, T, mult·d_model)
  • Output: (B, T, d_model)

Flow:

  1. Linear up-projection to width mult·d_model
  2. Nonlinearity: GELU (smooth, commonly used in GPT-style blocks)
  3. Linear down-projection back to d_model
  4. Dropout for regularization

Notes:

  • Same FFN weights are used for all positions; no mixing across time here
  • Residual connections are added around FFN in the Transformer block
class FeedForward(nn.Module):
    def __init__(self, d_model: int, mult: int = 4, dropout: float = 0.0):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(d_model, mult * d_model),
            nn.GELU(),
            nn.Linear(mult * d_model, d_model),
            nn.Dropout(dropout),
        )

    def forward(self, x):
        return self.net(x)


# Quick demo
x = torch.randn(2, 5, 12)
ffn = FeedForward(12, mult=4, dropout=0.1)
print("FFN out:", ffn(x).shape)
FFN out: torch.Size([2, 5, 12])

Transformer block

Pre-norm block: normalize first, apply sublayer, then add residual.

Flow and shapes (all (B, T, d_model)):

  1. x1 = LN1(x)
  2. attn_out, _ = MHA(x1); residual: x = x + attn_out
  3. x2 = LN2(x)
  4. ffn_out = FFN(x2); residual: x = x + ffn_out

Notes and rationale:

  • Pre-norm (LN before each sublayer) stabilizes training in deep Transformers
  • Residual paths help gradient flow and preserve input information
  • Dropout is typically applied inside MHA/FFN; shapes remain (B, T, d_model) throughout
class TransformerBlock(nn.Module):
    def __init__(self, d_model: int, n_head: int, dropout: float = 0.0):
        super().__init__()
        self.ln1 = nn.LayerNorm(d_model)
        self.attn = MultiHeadSelfAttention(d_model, n_head, dropout)
        self.ln2 = nn.LayerNorm(d_model)
        self.ffn = FeedForward(d_model, mult=4, dropout=dropout)

    def forward(self, x):
        x = x + self.attn(self.ln1(x))[0]
        x = x + self.ffn(self.ln2(x))
        return x


# Quick demo
x = torch.randn(2, 6, 24)
block = TransformerBlock(d_model=24, n_head=4, dropout=0.1)
print("Block out:", block(x).shape)
Block out: torch.Size([2, 6, 24])

Shape walkthrough and quick visualization

Reading the prints:

  • qkv: (B,T,3*C): one linear builds Q|K|V concatenated
  • view → (B,T,3,H,D): split dimension for heads
  • q,k,v: (B,T,H,D) then transpose to (B,H,T,D) for batched matmuls
  • scores: (B,H,T,T); softmax over the last dim gives per-query distributions
  • ctx: (B,H,T,D); weighted sums of values
  • merge heads: (B,T,C) via transpose(1,2).contiguous().view(...)
  • final proj: (B,T,C) linear mixing across head outputs

Heatmap: rows are queries, columns are keys; brighter = higher attention weight. A strict upper triangle is near-zero due to the causal mask.

# Walkthrough shapes for MHA
B, T, d_model, n_head = 1, 5, 12, 3
x = torch.randn(B, T, d_model)
attn = MultiHeadSelfAttention(d_model, n_head, trace_shapes=False)

# Manually step through qkv path
qkv = attn.qkv(x)  # (B,T,3*d_model)
print("qkv:", tuple(qkv.shape))

d_head = d_model // n_head
qkv = qkv.view(B, T, 3, n_head, d_head)
print("view ->", tuple(qkv.shape))

q, k, v = qkv.unbind(dim=2)
print("q,k,v:", q.shape, k.shape, v.shape)

q = q.transpose(1, 2)
k = k.transpose(1, 2)
v = v.transpose(1, 2)
print("transpose heads:", q.shape, k.shape, v.shape)

scale = 1.0 / math.sqrt(d_head)
scores = torch.matmul(q, k.transpose(-2, -1)) * scale
print("scores:", scores.shape)
weights = torch.softmax(scores, dim=-1)
print("weights:", weights.shape)
ctx = torch.matmul(weights, v)
print("ctx:", ctx.shape)

out = ctx.transpose(1, 2).contiguous().view(B, T, d_model)
print("merge heads:", out.shape)
out = attn.proj(out)
print("final proj:", out.shape)
qkv: (1, 5, 36)
view -> (1, 5, 3, 3, 4)
q,k,v: torch.Size([1, 5, 3, 4]) torch.Size([1, 5, 3, 4]) torch.Size([1, 5, 3, 4])
transpose heads: torch.Size([1, 3, 5, 4]) torch.Size([1, 3, 5, 4]) torch.Size([1, 3, 5, 4])
scores: torch.Size([1, 3, 5, 5])
weights: torch.Size([1, 3, 5, 5])
ctx: torch.Size([1, 3, 5, 4])
merge heads: torch.Size([1, 5, 12])
final proj: torch.Size([1, 5, 12])
# Quick attention visualization for one head
import matplotlib.pyplot as plt

B, T, d_model, n_head = 1, 10, 24, 4
x = torch.randn(B, T, d_model)
attn = MultiHeadSelfAttention(d_model, n_head)
_, w = attn(x)  # (B,H,T,T)

head_idx = 0
w_head = w[0, head_idx].detach().cpu().numpy()
plt.imshow(w_head, cmap="viridis")
plt.title(f"Attention weights (head {head_idx})")
plt.xlabel("Key positions")
plt.ylabel("Query positions")
plt.colorbar()
plt.show()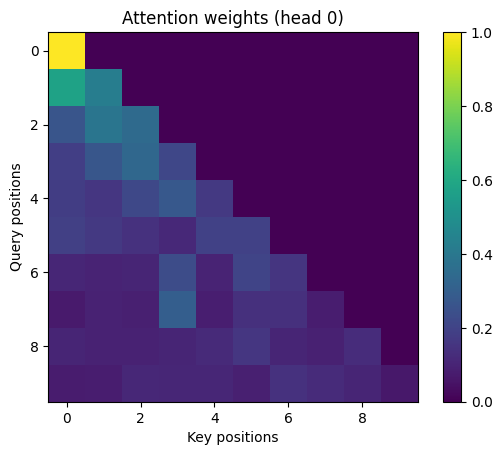

Attention weights

  • What was formed: The tensor w = softmax(scores, dim=-1) after causal masking (and then dropout during training). Its shape is (B, H, T, T). The plot shows one head: w[0, head_idx] of shape (T, T).
  • What each entry means: For row i (query position i), column j (key position j) is the probability that token i attends to token j. Each row is a distribution over keys for a single query.
  • Causal mask: The upper-right triangle is zero because future positions are disallowed; the model can only look at current and past tokens.
  • Row sums: With softmax, each row sums to 1. If attention dropout is applied after softmax (w = self.dropout(w)), exact row sums can be < 1 during training; in eval (or with dropout=0) rows sum to 1 up to floating‑point error.
  • How it’s used: Context at position i is a weighted sum of values: (c_i = _j w[i, j], v_j). Brighter cells mean larger contribution from v_j to c_i.
  • How to read the plot:
    • Bright diagonal → strong self/nearby attention.
    • Off-diagonal bright spots → dependencies on earlier tokens (e.g., delimiters, matching brackets).
    • Columns that are broadly bright → tokens influential across many positions.
    • First row can only attend to itself (nothing before it).

Reference:

  • https://medium.com/@vanshkharidia7/understanding-transformers-from-scratch-in-depth-fc8e760e02bb
  • https://www.youtube.com/watch?v=p3sij8QzONQ&t=13459s