Variationally Inferred Parameterization

Tutorial also hosted on Numpyro

Occasionally, the Hamiltonian Monte Carlo (HMC) sampler encounters challenges in effectively sampling from the posterior distribution. One illustrative case is Neal’s funnel. In these situations, the conventional centered parameterization may prove inadequate, leading us to employ non-centered parameterization. However, there are instances where even non-centered parameterization may not suffice, necessitating the utilization of Variationally Inferred Parameterization to attain the desired centeredness within the range of 0 to 1.

The purpose of this tutorial is to implement Variationally Inferred Parameterization based on Automatic Reparameterization of Probabilistic Programs using LocScaleReparam in Numpyro.

# %pip -qq install numpyro
# %pip -qq install ucimlrepo

import jax
import numpyro
import arviz as az
import numpy as np
import pandas as pd
import jax.numpy as jnp
from numpyro.infer import MCMC, NUTS
import numpyro.distributions as dist
from ucimlrepo import fetch_ucirepo

rng_key = jax.random.PRNGKey(0)
# from numpyro.infer.reparam import LocScaleReparam
from numpyro.infer import SVI, Trace_ELBO
from numpyro.infer.autoguide import AutoDiagonalNormal

WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1703315439.052736       1 tfrt_cpu_pjrt_client.cc:349] TfrtCpuClient created.

from numpyro.distributions import biject_to, constraints, Distribution
from numpyro.distributions.util import is_identically_one, safe_normalize, sum_rightmost
from numpyro.infer.reparam import Reparam
from numpyro.util import not_jax_tracer

class LocScaleReparam(Reparam):
    def __init__(self, centered=None, shape_params=()):
        assert centered is None or isinstance(
            centered, (int, float, np.generic, np.ndarray, jnp.ndarray, jax.core.Tracer)
        )
        assert isinstance(shape_params, (tuple, list))
        assert all(isinstance(name, str) for name in shape_params)
        if centered is not None:
            is_valid = constraints.unit_interval.check(centered)
            if not_jax_tracer(is_valid):
                if not np.all(is_valid):
                    raise ValueError(
                        "`centered` argument does not satisfy `0 <= centered <= 1`."
                    )

        self.centered = centered
        self.shape_params = shape_params

    def __call__(self, name, fn, obs):
        assert obs is None, "LocScaleReparam does not support observe statements"
        support = fn.support
        if isinstance(support, constraints.independent):
            support = fn.support.base_constraint
        if support is not constraints.real:
            raise ValueError(
                "LocScaleReparam only supports distributions with real "
                f"support, but got {support} support at site {name}."
            )

        centered = self.centered
        if is_identically_one(centered):
            return fn, obs
        event_shape = fn.event_shape
        fn, expand_shape, event_dim = self._unwrap(fn)

        # Apply a partial decentering transform.
        params = {key: getattr(fn, key) for key in self.shape_params}
        if self.centered is None:
            centered = numpyro.param(
                "{}_centered".format(name),
                jnp.full(event_shape, 0.5),
                constraint=constraints.unit_interval,
            )
        if isinstance(centered, (int, float, np.generic)) and centered == 0.0:
            params["loc"] = jnp.zeros_like(fn.loc)
            params["scale"] = jnp.ones_like(fn.scale)
        else:
            params["loc"] = fn.loc * centered
            params["scale"] = fn.scale**centered
        decentered_fn = self._wrap(type(fn)(**params), expand_shape, event_dim)

        # Draw decentered noise.
        decentered_value = numpyro.sample("{}_decentered".format(name), decentered_fn)

        # Differentiably transform.
        delta = decentered_value - centered * fn.loc
        value = fn.loc + jnp.power(fn.scale, 1 - centered) * delta

        # Simulate a pyro.deterministic() site.
        return None, value

1. Dataset

We will be using the German Credit Dataset for this illustration. The dataset consists of 1000 entries with 20 categorial symbolic attributes prepared by Prof. Hofmann. In this dataset, each entry represents a person who takes a credit by a bank. Each person is classified as good or bad credit risks according to the set of attributes.

def load_german_credit():
    statlog_german_credit_data = fetch_ucirepo(id=144)
    X = statlog_german_credit_data.data.features
    y = statlog_german_credit_data.data.targets
    return X, y

X, y = load_german_credit()
X

	Attribute1	Attribute2	Attribute3	Attribute4	Attribute5	Attribute6	Attribute7	Attribute8	Attribute9	Attribute10	Attribute11	Attribute12	Attribute13	Attribute14	Attribute15	Attribute16	Attribute17	Attribute18	Attribute19	Attribute20
0	A11	6	A34	A43	1169	A65	A75	4	A93	A101	4	A121	67	A143	A152	2	A173	1	A192	A201
1	A12	48	A32	A43	5951	A61	A73	2	A92	A101	2	A121	22	A143	A152	1	A173	1	A191	A201
2	A14	12	A34	A46	2096	A61	A74	2	A93	A101	3	A121	49	A143	A152	1	A172	2	A191	A201
3	A11	42	A32	A42	7882	A61	A74	2	A93	A103	4	A122	45	A143	A153	1	A173	2	A191	A201
4	A11	24	A33	A40	4870	A61	A73	3	A93	A101	4	A124	53	A143	A153	2	A173	2	A191	A201
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
995	A14	12	A32	A42	1736	A61	A74	3	A92	A101	4	A121	31	A143	A152	1	A172	1	A191	A201
996	A11	30	A32	A41	3857	A61	A73	4	A91	A101	4	A122	40	A143	A152	1	A174	1	A192	A201
997	A14	12	A32	A43	804	A61	A75	4	A93	A101	4	A123	38	A143	A152	1	A173	1	A191	A201
998	A11	45	A32	A43	1845	A61	A73	4	A93	A101	4	A124	23	A143	A153	1	A173	1	A192	A201
999	A12	45	A34	A41	4576	A62	A71	3	A93	A101	4	A123	27	A143	A152	1	A173	1	A191	A201

1000 rows × 20 columns

Here, X depicts 20 attributes and the values corresponding to these attributes for each person represented in the data entry and y is the output variable corresponding to these attributes

def data_transform(X, y):
    def categorical_to_int(x):
        d = {u: i for i, u in enumerate(np.unique(x))}
        return np.array([d[i] for i in x])

    categoricals = []
    numericals = []
    numericals.append(np.ones([len(y)]))
    for column in X:
        column = X[column]
        if column.dtype == "O":
            categoricals.append(categorical_to_int(column))
        else:
            numericals.append((column - column.mean()) / column.std())
    numericals = np.array(numericals).T
    status = np.array(y == 1, dtype=np.int32)
    status = np.squeeze(status)

    return jnp.array(numericals), jnp.array(categoricals), jnp.array(status)

Data transformation for feeding it into the Numpyro model

numericals, categoricals, status = data_transform(X, y)

x_numeric = numericals.astype(jnp.float32)
x_categorical = [jnp.eye(c.max() + 1)[c] for c in categoricals]
all_x = jnp.concatenate([x_numeric] + x_categorical, axis=1)
num_features = all_x.shape[1]
y = status[jnp.newaxis, Ellipsis]

2. Model

We will be using a logistic regression model with hierarchical prior on coefficient scales

\[\begin{aligned} \log \tau_0 & \sim \mathcal{N}(0,10) & \log \tau_i & \sim \mathcal{N}\left(\log \tau_0, 1\right) \\ \beta_i & \sim \mathcal{N}\left(0, \tau_i\right) & y & \sim \operatorname{Bernoulli}\left(\sigma\left(\beta X^T\right)\right) \end{aligned}\]

def german_credit():
    log_tau_zero = numpyro.sample("log_tau_zero", dist.Normal(0, 10))
    log_tau_i = numpyro.sample(
        "log_tau_i", dist.Normal(log_tau_zero, jnp.ones(num_features))
    )
    beta = numpyro.sample(
        "beta", dist.Normal(jnp.zeros(num_features), jnp.exp(log_tau_i))
    )
    numpyro.sample(
        "obs",
        dist.Bernoulli(logits=jnp.einsum("nd,md->mn", all_x, beta[jnp.newaxis, :])),
        obs=y,
    )

nuts_kernel = NUTS(german_credit)
mcmc = MCMC(nuts_kernel, num_warmup=1000, num_samples=1000)
mcmc.run(rng_key, extra_fields=("num_steps",))

sample: 100%|██████████| 2000/2000 [00:05<00:00, 390.49it/s, 63 steps of size 9.48e-02. acc. prob=0.76]

mcmc.print_summary()


                    mean       std    median      5.0%     95.0%     n_eff     r_hat
       beta[0]      0.16      0.45      0.06     -0.52      0.73    175.35      1.01
       beta[1]     -0.33      0.11     -0.34     -0.51     -0.15    402.52      1.00
       beta[2]     -0.28      0.13     -0.28     -0.49     -0.07    326.71      1.00
       beta[3]     -0.29      0.10     -0.30     -0.46     -0.14    385.57      1.00
       beta[4]     -0.01      0.07     -0.01     -0.12      0.09    630.59      1.00
       beta[5]      0.12      0.09      0.12     -0.01      0.28    520.89      1.00
       beta[6]     -0.09      0.09     -0.08     -0.24      0.04    528.06      1.00
       beta[7]     -0.04      0.08     -0.04     -0.17      0.08    468.54      1.00
       beta[8]     -0.42      0.35     -0.37     -0.95      0.08    128.69      1.00
       beta[9]     -0.06      0.28     -0.02     -0.46      0.46    127.10      1.00
      beta[10]      0.28      0.35      0.19     -0.19      0.84    178.28      1.00
      beta[11]      1.25      0.36      1.29      0.69      1.82    117.82      1.00
      beta[12]     -0.27      0.35     -0.18     -0.87      0.18    442.81      1.00
      beta[13]     -0.31      0.34     -0.22     -0.83      0.20    318.44      1.01
      beta[14]      0.07      0.21      0.04     -0.19      0.48    247.56      1.00
      beta[15]      0.12      0.23      0.07     -0.20      0.53    241.17      1.00
      beta[16]      0.77      0.31      0.76      0.25      1.28    262.78      1.00
      beta[17]     -0.54      0.27     -0.55     -1.00     -0.12    303.51      1.00
      beta[18]      0.71      0.43      0.71     -0.02      1.32    302.30      1.00
      beta[19]      0.13      0.37      0.04     -0.43      0.72    214.82      1.01
      beta[20]      0.03      0.17      0.01     -0.23      0.32    403.52      1.00
      beta[21]      0.16      0.20      0.12     -0.15      0.47    331.40      1.00
      beta[22]     -0.04      0.35     -0.00     -0.58      0.45    309.27      1.00
      beta[23]     -0.14      0.31     -0.05     -0.65      0.25    274.21      1.01
      beta[24]     -0.34      0.37     -0.24     -0.95      0.15    356.72      1.00
      beta[25]      0.17      0.43      0.05     -0.49      0.85    240.65      1.00
      beta[26]     -0.01      0.18     -0.01     -0.33      0.25    463.33      1.00
      beta[27]     -0.40      0.27     -0.40     -0.77      0.08    227.41      1.00
      beta[28]     -0.09      0.24     -0.04     -0.46      0.28    313.28      1.00
      beta[29]      0.00      0.22     -0.00     -0.34      0.34    274.70      1.00
      beta[30]      0.31      0.40      0.20     -0.24      0.97    389.17      1.00
      beta[31]      0.35      0.32      0.31     -0.09      0.87    194.82      1.00
      beta[32]     -0.02      0.20     -0.01     -0.39      0.25    367.68      1.01
      beta[33]     -0.13      0.19     -0.09     -0.39      0.18    304.34      1.00
      beta[34]     -0.03      0.16     -0.02     -0.27      0.24    314.53      1.00
      beta[35]      0.42      0.27      0.42     -0.00      0.82    342.84      1.00
      beta[36]      0.05      0.17      0.03     -0.22      0.33    270.04      1.00
      beta[37]     -0.11      0.24     -0.06     -0.50      0.19    293.60      1.00
      beta[38]     -0.07      0.19     -0.05     -0.38      0.23    353.75      1.00
      beta[39]      0.36      0.25      0.35     -0.03      0.74    304.10      1.00
      beta[40]      0.05      0.20      0.02     -0.27      0.37    352.03      1.00
      beta[41]     -0.01      0.21     -0.02     -0.31      0.38    286.79      1.00
      beta[42]     -0.11      0.25     -0.05     -0.54      0.27    329.03      1.00
      beta[43]      0.58      0.47      0.50     -0.08      1.32    265.76      1.00
      beta[44]      0.19      0.20      0.15     -0.10      0.53    293.58      1.00
      beta[45]     -0.01      0.16     -0.01     -0.28      0.24    329.91      1.00
      beta[46]      0.01      0.17      0.00     -0.32      0.25    151.24      1.00
      beta[47]     -0.21      0.27     -0.14     -0.64      0.19    175.35      1.00
      beta[48]     -0.11      0.24     -0.06     -0.54      0.22    237.31      1.00
      beta[49]     -0.04      0.22     -0.02     -0.42      0.28    384.71      1.00
      beta[50]      0.39      0.29      0.38     -0.05      0.83    283.57      1.00
      beta[51]     -0.17      0.22     -0.13     -0.54      0.13    264.01      1.00
      beta[52]      0.17      0.20      0.14     -0.10      0.51    306.17      1.00
      beta[53]      0.09      0.24      0.03     -0.28      0.48    233.69      1.00
      beta[54]      0.04      0.23      0.02     -0.30      0.45    560.22      1.00
      beta[55]      0.01      0.15      0.01     -0.23      0.24    605.75      1.00
      beta[56]     -0.01      0.13     -0.01     -0.24      0.21    612.61      1.00
      beta[57]     -0.01      0.17     -0.01     -0.29      0.26    380.62      1.00
      beta[58]     -0.06      0.19     -0.04     -0.39      0.21    284.09      1.01
      beta[59]      0.15      0.21      0.11     -0.11      0.51    284.56      1.00
      beta[60]     -0.13      0.33     -0.05     -0.62      0.39    208.99      1.01
      beta[61]      0.53      0.57      0.38     -0.17      1.45    242.27      1.00
  log_tau_i[0]     -1.45      0.96     -1.44     -2.82      0.27    227.43      1.00
  log_tau_i[1]     -1.06      0.64     -1.12     -2.01     -0.05    554.22      1.00
  log_tau_i[2]     -1.20      0.73     -1.19     -2.27      0.07    490.61      1.00
  log_tau_i[3]     -1.16      0.68     -1.18     -2.32     -0.08    419.73      1.00
  log_tau_i[4]     -2.09      0.89     -2.12     -3.53     -0.55    475.61      1.00
  log_tau_i[5]     -1.68      0.78     -1.68     -2.85     -0.30    582.02      1.00
  log_tau_i[6]     -1.82      0.88     -1.83     -3.11     -0.18    461.32      1.01
  log_tau_i[7]     -1.99      0.91     -2.00     -3.37     -0.42    349.52      1.00
  log_tau_i[8]     -1.01      0.86     -0.96     -2.32      0.34    186.45      1.00
  log_tau_i[9]     -1.55      0.88     -1.53     -2.91     -0.11    344.53      1.00
 log_tau_i[10]     -1.27      0.93     -1.22     -2.84      0.13    316.71      1.01
 log_tau_i[11]     -0.06      0.59     -0.06     -0.82      1.08    238.35      1.00
 log_tau_i[12]     -1.28      0.91     -1.23     -2.87      0.15    424.21      1.00
 log_tau_i[13]     -1.24      0.92     -1.17     -2.64      0.26    440.32      1.01
 log_tau_i[14]     -1.67      0.89     -1.66     -3.08     -0.10    293.72      1.01
 log_tau_i[15]     -1.62      0.93     -1.56     -3.31     -0.21    328.74      1.01
 log_tau_i[16]     -0.50      0.63     -0.48     -1.56      0.47    361.89      1.00
 log_tau_i[17]     -0.79      0.71     -0.75     -1.93      0.36    333.02      1.00
 log_tau_i[18]     -0.64      0.84     -0.57     -2.06      0.62    334.29      1.00
 log_tau_i[19]     -1.48      0.98     -1.44     -2.95      0.23    170.72      1.01
 log_tau_i[20]     -1.83      0.91     -1.81     -3.40     -0.48    491.17      1.00
 log_tau_i[21]     -1.53      0.90     -1.54     -2.87      0.03    410.15      1.00
 log_tau_i[22]     -1.55      0.99     -1.54     -3.23      0.01    261.14      1.00
 log_tau_i[23]     -1.60      0.92     -1.59     -3.12     -0.20    308.73      1.01
 log_tau_i[24]     -1.20      0.97     -1.11     -2.89      0.31    295.55      1.00
 log_tau_i[25]     -1.42      0.97     -1.37     -3.15     -0.05    218.51      1.00
 log_tau_i[26]     -1.76      0.86     -1.71     -3.24     -0.40    423.96      1.00
 log_tau_i[27]     -1.04      0.82     -0.99     -2.36      0.28    326.90      1.00
 log_tau_i[28]     -1.65      0.96     -1.61     -3.21     -0.09    325.98      1.01
 log_tau_i[29]     -1.69      0.89     -1.70     -2.98     -0.01    418.01      1.00
 log_tau_i[30]     -1.24      0.97     -1.23     -3.00      0.26    309.77      1.00
 log_tau_i[31]     -1.16      0.94     -1.03     -2.93      0.13    352.52      1.01
 log_tau_i[32]     -1.75      0.97     -1.71     -3.30     -0.15    392.45      1.00
 log_tau_i[33]     -1.57      0.85     -1.54     -2.99     -0.23    420.93      1.00
 log_tau_i[34]     -1.81      0.93     -1.81     -3.48     -0.40    272.61      1.00
 log_tau_i[35]     -1.01      0.79     -0.93     -2.33      0.18    427.14      1.00
 log_tau_i[36]     -1.71      0.85     -1.69     -3.19     -0.42    277.28      1.00
 log_tau_i[37]     -1.57      0.97     -1.56     -2.96      0.31    371.83      1.00
 log_tau_i[38]     -1.65      0.88     -1.62     -3.03     -0.22    474.97      1.00
 log_tau_i[39]     -1.11      0.89     -1.06     -2.63      0.27    246.36      1.00
 log_tau_i[40]     -1.70      0.89     -1.68     -3.07     -0.26    356.11      1.00
 log_tau_i[41]     -1.73      0.91     -1.73     -3.13     -0.06    333.35      1.00
 log_tau_i[42]     -1.57      0.89     -1.58     -2.97     -0.07    338.73      1.00
 log_tau_i[43]     -0.84      0.91     -0.73     -2.22      0.63    305.01      1.00
 log_tau_i[44]     -1.48      0.93     -1.42     -2.95      0.04    338.51      1.00
 log_tau_i[45]     -1.81      0.89     -1.81     -3.10     -0.21    386.99      1.00
 log_tau_i[46]     -1.76      0.93     -1.72     -3.41     -0.34    368.09      1.00
 log_tau_i[47]     -1.45      0.92     -1.44     -3.07     -0.03    325.43      1.00
 log_tau_i[48]     -1.58      0.91     -1.56     -3.11     -0.21    273.83      1.01
 log_tau_i[49]     -1.71      0.94     -1.68     -3.48     -0.37    256.16      1.00
 log_tau_i[50]     -1.07      0.88     -1.01     -2.51      0.36    275.10      1.00
 log_tau_i[51]     -1.51      0.89     -1.50     -2.91     -0.05    417.23      1.00
 log_tau_i[52]     -1.56      0.88     -1.51     -2.96     -0.11    341.36      1.00
 log_tau_i[53]     -1.72      0.90     -1.71     -3.09     -0.16    294.87      1.00
 log_tau_i[54]     -1.69      0.91     -1.67     -3.11     -0.18    291.98      1.00
 log_tau_i[55]     -1.87      0.92     -1.86     -3.47     -0.46    526.89      1.00
 log_tau_i[56]     -1.86      0.91     -1.85     -3.39     -0.39    497.99      1.00
 log_tau_i[57]     -1.84      0.87     -1.83     -3.24     -0.42    385.89      1.00
 log_tau_i[58]     -1.70      0.93     -1.68     -3.27     -0.29    530.10      1.00
 log_tau_i[59]     -1.58      0.90     -1.56     -3.18     -0.24    475.23      1.00
 log_tau_i[60]     -1.52      0.95     -1.50     -3.32     -0.26    273.32      1.00
 log_tau_i[61]     -0.94      1.01     -0.83     -2.69      0.51    241.57      1.00
  log_tau_zero     -1.45      0.24     -1.45     -1.80     -1.02    155.67      1.00

Number of divergences: 61

From mcmc.print_summary it is evident that there are 37 divergences. Thus, we will use Variationally Inferred Parameterization (VIP) to reduce these divergences

data = az.from_numpyro(mcmc)
az.plot_trace(data, compact=True);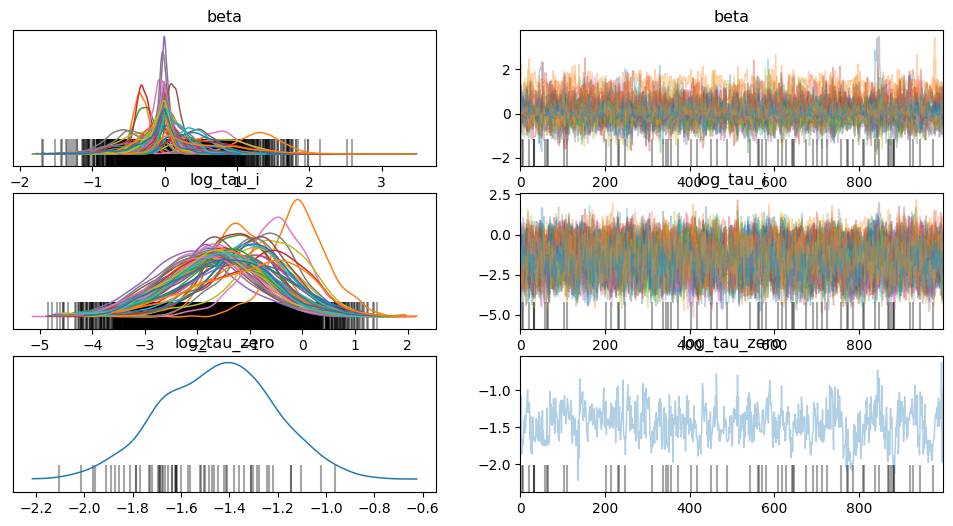

3. Reparameterization

We introduce a parameterization parameters \(\lambda \in [0,1]\) for any variable \(z\), and transform:

=> \(z\) ~ \(N (z | μ, σ)\)

=> by defining \(z\) ~ \(N(λμ, σ^λ)\)

=> \(z\) = \(μ + σ^{1-λ}(z - λμ)\).

Thus, using the above transformation the joint density can be transformed as follows: \[\begin{aligned} p(\theta, \hat{\mu}, \mathbf{y}) & =\mathcal{N}(\theta \mid 0,1) \times \mathcal{N}\left(\mu \mid \theta, \sigma_\mu\right) \times \mathcal{N}(\mathbf{y} \mid \mu, \sigma) \end{aligned}\] \[\begin{aligned} p(\theta, \hat{\mu}, \mathbf{y}) & =\mathcal{N}(\theta \mid 0,1) \times \mathcal{N}\left(\hat{\mu} \mid \lambda \theta, \sigma_\mu^\lambda\right) \times \mathcal{N}\left(\mathbf{y} \mid \theta+\sigma_\mu^{1-\lambda}(\hat{\mu}-\lambda \theta), \sigma\right) \end{aligned}\]

def german_credit_reparam(beta_centeredness=None):
    def model():
        log_tau_zero = numpyro.sample("log_tau_zero", dist.Normal(0, 10))
        log_tau_i = numpyro.sample(
            "log_tau_i", dist.Normal(log_tau_zero, jnp.ones(num_features))
        )
        with numpyro.handlers.reparam(
            config={"beta": LocScaleReparam(beta_centeredness)}
        ):
            beta = numpyro.sample(
                "beta", dist.Normal(jnp.zeros(num_features), jnp.exp(log_tau_i))
            )
        numpyro.sample(
            "obs",
            dist.Bernoulli(logits=jnp.einsum("nd,md->mn", all_x, beta[jnp.newaxis, :])),
            obs=y,
        )
    return model

Now, using SVI we optimize \(\lambda\).

model = german_credit_reparam()
guide = AutoDiagonalNormal(model)
svi = SVI(model, guide, numpyro.optim.Adam(3e-4), Trace_ELBO(10))
svi_results = svi.run(rng_key, 10000)

100%|██████████| 10000/10000 [00:05<00:00, 1903.74it/s, init loss: 2165.2427, avg. loss [9501-10000]: 576.7846]

reparam_model = german_credit_reparam(
    beta_centeredness=svi_results.params["beta_centered"]
)

nuts_kernel = NUTS(reparam_model)
mcmc_reparam = MCMC(nuts_kernel, num_warmup=1000, num_samples=1000)
mcmc_reparam.run(rng_key, extra_fields=("num_steps",))

sample: 100%|██████████| 2000/2000 [00:04<00:00, 482.98it/s, 31 steps of size 1.10e-01. acc. prob=0.93]

mcmc_reparam.get_samples().keys()

dict_keys(['beta', 'beta_decentered', 'log_tau_i', 'log_tau_zero'])

mcmc_reparam.print_summary()


                         mean       std    median      5.0%     95.0%     n_eff     r_hat
 beta_decentered[0]      0.13      0.42      0.06     -0.54      0.78    275.93      1.00
 beta_decentered[1]     -0.46      0.15     -0.45     -0.70     -0.21    640.20      1.00
 beta_decentered[2]     -0.37      0.17     -0.37     -0.66     -0.08    532.24      1.00
 beta_decentered[3]     -0.41      0.14     -0.41     -0.62     -0.16    729.70      1.00
 beta_decentered[4]     -0.01      0.12     -0.01     -0.19      0.20    893.99      1.00
 beta_decentered[5]      0.19      0.14      0.19     -0.01      0.42    878.97      1.00
 beta_decentered[6]     -0.13      0.14     -0.13     -0.38      0.07    938.88      1.00
 beta_decentered[7]     -0.07      0.12     -0.06     -0.26      0.13    810.45      1.00
 beta_decentered[8]     -0.46      0.33     -0.47     -0.95      0.09    278.11      1.00
 beta_decentered[9]     -0.02      0.32     -0.02     -0.53      0.51    253.14      1.00
beta_decentered[10]      0.35      0.39      0.28     -0.20      0.99    297.60      1.00
beta_decentered[11]      1.30      0.31      1.31      0.81      1.78    304.84      1.00
beta_decentered[12]     -0.31      0.39     -0.26     -0.94      0.28    551.22      1.00
beta_decentered[13]     -0.39      0.39     -0.33     -1.01      0.22    336.39      1.00
beta_decentered[14]      0.08      0.27      0.06     -0.32      0.54    364.10      1.00
beta_decentered[15]      0.13      0.29      0.10     -0.33      0.61    527.76      1.00
beta_decentered[16]      0.85      0.31      0.86      0.30      1.32    391.70      1.00
beta_decentered[17]     -0.64      0.28     -0.65     -1.11     -0.18    434.17      1.00
beta_decentered[18]      0.78      0.42      0.81      0.11      1.49    391.42      1.00
beta_decentered[19]      0.15      0.41      0.09     -0.45      0.91    447.14      1.00
beta_decentered[20]      0.04      0.23      0.02     -0.36      0.41    354.95      1.00
beta_decentered[21]      0.23      0.26      0.21     -0.15      0.65    429.67      1.00
beta_decentered[22]     -0.04      0.37     -0.02     -0.65      0.53    808.59      1.00
beta_decentered[23]     -0.15      0.33     -0.08     -0.66      0.41    456.72      1.01
beta_decentered[24]     -0.40      0.39     -0.34     -1.05      0.20    596.39      1.00
beta_decentered[25]      0.18      0.46      0.11     -0.59      0.89    452.92      1.00
beta_decentered[26]     -0.00      0.25      0.01     -0.42      0.39    579.03      1.00
beta_decentered[27]     -0.47      0.31     -0.48     -0.91      0.07    245.48      1.00
beta_decentered[28]     -0.10      0.31     -0.06     -0.58      0.42    387.49      1.00
beta_decentered[29]      0.01      0.29     -0.00     -0.53      0.45    478.36      1.00
beta_decentered[30]      0.38      0.43      0.29     -0.21      1.08    450.02      1.00
beta_decentered[31]      0.46      0.36      0.44     -0.11      1.02    299.64      1.00
beta_decentered[32]     -0.03      0.26     -0.02     -0.45      0.44    548.53      1.00
beta_decentered[33]     -0.17      0.24     -0.15     -0.60      0.20    507.06      1.00
beta_decentered[34]     -0.02      0.21     -0.02     -0.34      0.36    499.13      1.00
beta_decentered[35]      0.54      0.30      0.55      0.04      1.01    578.79      1.00
beta_decentered[36]      0.09      0.24      0.07     -0.31      0.46    487.44      1.00
beta_decentered[37]     -0.15      0.32     -0.10     -0.71      0.31    526.21      1.00
beta_decentered[38]     -0.13      0.26     -0.11     -0.59      0.27    351.97      1.00
beta_decentered[39]      0.43      0.27      0.42     -0.02      0.84    383.33      1.00
beta_decentered[40]      0.05      0.26      0.04     -0.39      0.48    537.39      1.00
beta_decentered[41]      0.01      0.29      0.01     -0.43      0.49    376.65      1.00
beta_decentered[42]     -0.14      0.32     -0.09     -0.75      0.28    463.26      1.00
beta_decentered[43]      0.66      0.46      0.66     -0.03      1.46    416.53      1.01
beta_decentered[44]      0.25      0.26      0.24     -0.15      0.64    560.15      1.00
beta_decentered[45]     -0.01      0.22     -0.01     -0.39      0.35    606.91      1.00
beta_decentered[46]      0.01      0.23      0.01     -0.40      0.34    535.77      1.00
beta_decentered[47]     -0.24      0.31     -0.20     -0.73      0.24    432.11      1.00
beta_decentered[48]     -0.18      0.31     -0.15     -0.69      0.32    334.89      1.00
beta_decentered[49]     -0.06      0.29     -0.04     -0.52      0.44    491.70      1.00
beta_decentered[50]      0.46      0.31      0.48     -0.03      0.97    321.70      1.00
beta_decentered[51]     -0.23      0.27     -0.20     -0.64      0.23    367.02      1.01
beta_decentered[52]      0.22      0.26      0.20     -0.17      0.65    325.06      1.00
beta_decentered[53]      0.07      0.29      0.05     -0.46      0.53    580.63      1.00
beta_decentered[54]      0.04      0.30      0.03     -0.42      0.56    475.33      1.00
beta_decentered[55]      0.02      0.22      0.02     -0.30      0.39    803.43      1.00
beta_decentered[56]     -0.01      0.19     -0.02     -0.35      0.26    656.58      1.00
beta_decentered[57]      0.01      0.23      0.01     -0.32      0.43    540.58      1.01
beta_decentered[58]     -0.08      0.27     -0.08     -0.52      0.35    293.34      1.01
beta_decentered[59]      0.20      0.28      0.17     -0.23      0.64    325.75      1.01
beta_decentered[60]     -0.14      0.37     -0.09     -0.77      0.44    256.23      1.00
beta_decentered[61]      0.59      0.57      0.52     -0.23      1.45    381.03      1.00
       log_tau_i[0]     -1.54      0.95     -1.47     -3.31     -0.15    515.73      1.00
       log_tau_i[1]     -1.05      0.65     -1.10     -2.21     -0.12    770.10      1.00
       log_tau_i[2]     -1.22      0.74     -1.21     -2.41     -0.13    605.37      1.00
       log_tau_i[3]     -1.16      0.66     -1.16     -2.19     -0.03    658.53      1.00
       log_tau_i[4]     -2.09      0.87     -2.10     -3.50     -0.69    864.75      1.00
       log_tau_i[5]     -1.70      0.83     -1.68     -2.97     -0.29    756.87      1.00
       log_tau_i[6]     -1.86      0.91     -1.83     -3.30     -0.37   1082.11      1.00
       log_tau_i[7]     -2.03      0.92     -2.05     -3.65     -0.65    464.97      1.00
       log_tau_i[8]     -1.10      0.88     -1.04     -2.50      0.37    413.02      1.00
       log_tau_i[9]     -1.67      0.87     -1.65     -3.25     -0.43    633.18      1.00
      log_tau_i[10]     -1.34      0.96     -1.27     -3.00      0.15    437.87      1.00
      log_tau_i[11]     -0.03      0.49     -0.06     -0.78      0.81    490.94      1.00
      log_tau_i[12]     -1.35      0.97     -1.29     -2.80      0.27    597.46      1.00
      log_tau_i[13]     -1.27      0.96     -1.21     -2.85      0.24    591.98      1.00
      log_tau_i[14]     -1.73      0.94     -1.72     -3.22     -0.09    669.66      1.00
      log_tau_i[15]     -1.69      0.95     -1.65     -3.43     -0.28    571.40      1.00
      log_tau_i[16]     -0.52      0.64     -0.50     -1.56      0.56    515.69      1.00
      log_tau_i[17]     -0.80      0.67     -0.79     -2.00      0.21    558.88      1.00
      log_tau_i[18]     -0.70      0.83     -0.60     -1.89      0.76    506.17      1.00
      log_tau_i[19]     -1.54      0.98     -1.50     -3.37     -0.11    506.59      1.00
      log_tau_i[20]     -1.81      0.90     -1.78     -3.27     -0.36    662.64      1.00
      log_tau_i[21]     -1.55      0.93     -1.51     -3.09     -0.08    742.04      1.00
      log_tau_i[22]     -1.60      1.02     -1.54     -3.18      0.15    682.59      1.00
      log_tau_i[23]     -1.68      0.97     -1.62     -3.24     -0.14    453.56      1.00
      log_tau_i[24]     -1.23      0.94     -1.14     -2.69      0.32    599.87      1.00
      log_tau_i[25]     -1.50      1.04     -1.46     -3.08      0.38    381.49      1.00
      log_tau_i[26]     -1.77      0.92     -1.75     -3.29     -0.26    719.89      1.00
      log_tau_i[27]     -1.12      0.88     -1.05     -2.56      0.26    332.21      1.00
      log_tau_i[28]     -1.71      0.94     -1.68     -3.32     -0.24    653.14      1.01
      log_tau_i[29]     -1.68      0.94     -1.67     -3.24     -0.17    592.44      1.00
      log_tau_i[30]     -1.27      1.01     -1.20     -3.01      0.33    493.61      1.00
      log_tau_i[31]     -1.14      0.87     -1.04     -2.67      0.18    422.70      1.00
      log_tau_i[32]     -1.74      0.98     -1.76     -3.30     -0.20    543.91      1.00
      log_tau_i[33]     -1.65      0.89     -1.59     -3.04     -0.25    738.85      1.00
      log_tau_i[34]     -1.87      0.94     -1.83     -3.53     -0.39    585.19      1.00
      log_tau_i[35]     -0.98      0.82     -0.92     -2.18      0.48    632.48      1.00
      log_tau_i[36]     -1.75      0.92     -1.69     -3.26     -0.32    676.94      1.00
      log_tau_i[37]     -1.61      0.98     -1.58     -3.17      0.02    799.87      1.00
      log_tau_i[38]     -1.68      0.90     -1.64     -3.05     -0.20    584.27      1.00
      log_tau_i[39]     -1.16      0.85     -1.05     -2.58      0.13    564.75      1.00
      log_tau_i[40]     -1.73      0.92     -1.69     -3.07     -0.13    643.67      1.00
      log_tau_i[41]     -1.75      0.94     -1.76     -3.31     -0.32    577.68      1.00
      log_tau_i[42]     -1.62      0.91     -1.65     -3.19     -0.22    525.10      1.00
      log_tau_i[43]     -0.79      0.92     -0.74     -2.46      0.56    491.72      1.01
      log_tau_i[44]     -1.51      0.90     -1.50     -3.17     -0.22    894.90      1.00
      log_tau_i[45]     -1.84      0.91     -1.82     -3.22     -0.35    916.67      1.00
      log_tau_i[46]     -1.84      0.89     -1.77     -3.35     -0.45    880.63      1.00
      log_tau_i[47]     -1.53      0.93     -1.52     -3.17     -0.13    587.07      1.00
      log_tau_i[48]     -1.56      0.96     -1.50     -3.20     -0.08    541.89      1.00
      log_tau_i[49]     -1.72      0.93     -1.73     -3.33     -0.30    838.34      1.00
      log_tau_i[50]     -1.14      0.86     -1.06     -2.43      0.22    377.83      1.00
      log_tau_i[51]     -1.55      0.90     -1.53     -3.09     -0.13    585.07      1.00
      log_tau_i[52]     -1.61      0.90     -1.56     -3.02     -0.06    638.21      1.00
      log_tau_i[53]     -1.71      0.92     -1.68     -3.19     -0.22    634.97      1.00
      log_tau_i[54]     -1.75      0.93     -1.73     -3.17     -0.10    687.26      1.00
      log_tau_i[55]     -1.88      0.92     -1.90     -3.35     -0.30    995.19      1.00
      log_tau_i[56]     -1.89      0.93     -1.88     -3.25     -0.23    788.73      1.00
      log_tau_i[57]     -1.84      0.94     -1.83     -3.32     -0.20    832.65      1.00
      log_tau_i[58]     -1.73      0.95     -1.70     -3.29     -0.18    531.53      1.00
      log_tau_i[59]     -1.61      0.92     -1.57     -3.12     -0.16    524.50      1.00
      log_tau_i[60]     -1.58      0.97     -1.53     -3.07      0.04    408.84      1.00
      log_tau_i[61]     -0.97      1.03     -0.88     -2.59      0.71    435.12      1.00
       log_tau_zero     -1.49      0.25     -1.49     -1.90     -1.10    225.37      1.00

Number of divergences: 1

The number of divergences have significantly reduced from 37 to 1.

data = az.from_numpyro(mcmc_reparam)
az.plot_trace(data, compact=True, figsize=(15, 25));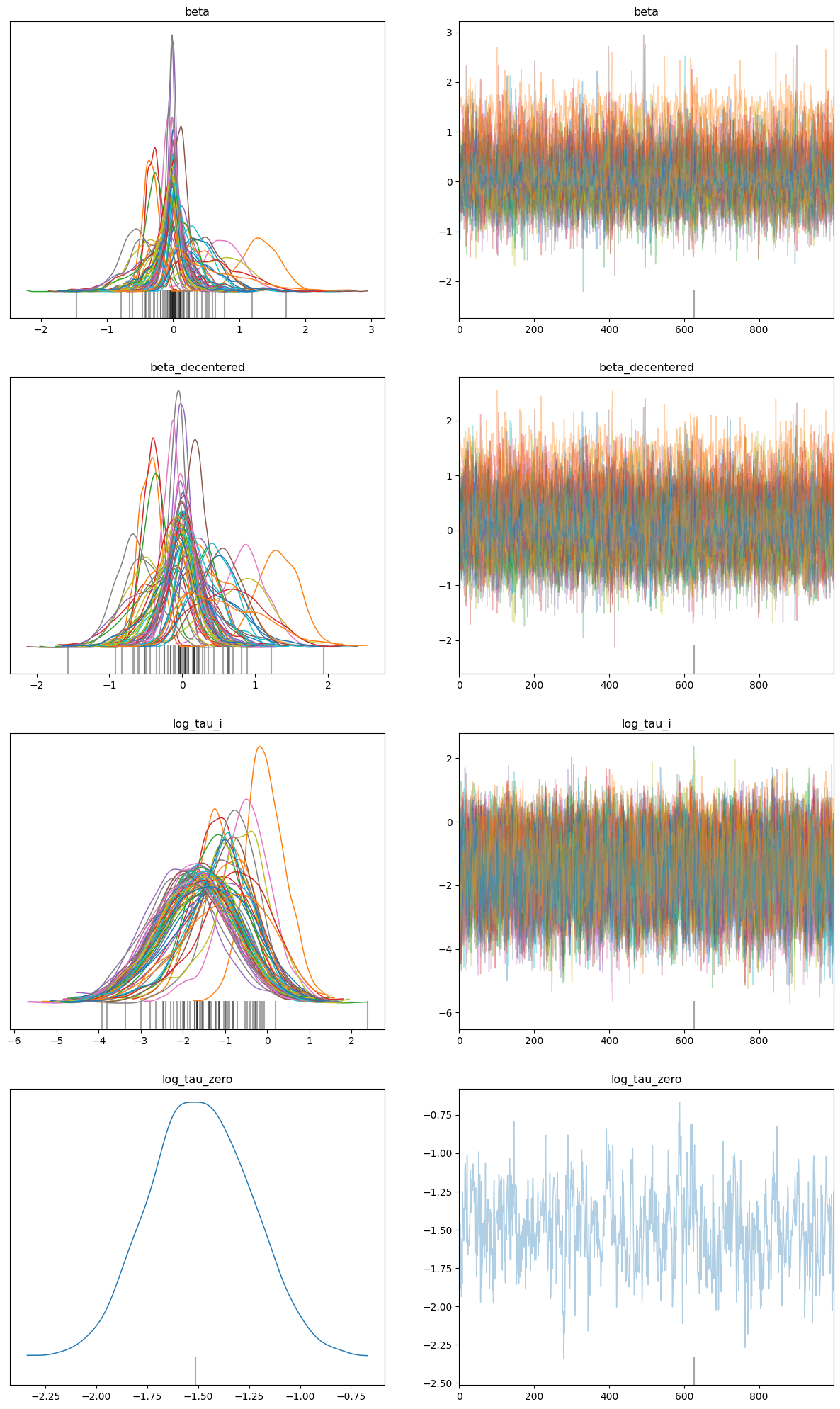

4. References:

https://arxiv.org/abs/1906.03028
https://github.com/mgorinova/autoreparam/tree/master